競プロっぽい所その(1) - 道路グラフを検証する処理

道路グラフとは何かと言うと、道の要所要所の座標や接続関係を表した有向グラフです。OSM(OpenStreetMap) データを元に作ります。

// 道路グラフ
 struct RoadGraph {
  vector<Vector3> 頂点配列
  vector<vector<int> > 隣接リスト
 }

いたって普通の隣接リスト表現です。

で、山手線をまるごと含むエリアの道路グラフは頂点数 82,474、辺数 115,738 で、図にするとこんなんです。

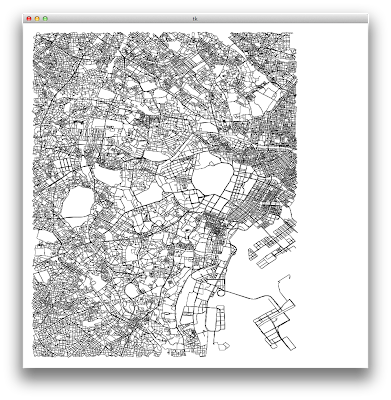
結構濃ゆいですね。いかにも TLE しそうな香りがします。

実はこの道路グラフ、馬場タク内のいろんな所で使われています。例えば：

• AI車がそれっぽい動きをするように道路グラフ上をランダムウォークさせる
• タクシーモードのとき、プレイヤーの現在地から目的地までの最短経路を A* で計算して表示する
• ガードレール、街路樹、放置自転車、ビルの看板、ジャンプ台、客の初期位置、AI車の初期位置など、各種データを道路グラフを元に生成する

などなど。

さてこの道路グラフですが、何しろ手動で入力された OSM データを元にしているので、素性の良さを検証したいと思います。

例えば、交差点は中央の頂点が図のように周囲の４頂点とつながっていることが期待されますが、

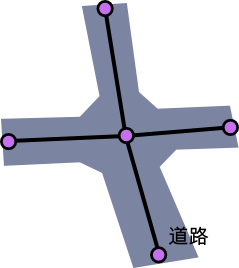
次の図のように交差点が別々の頂点に分かれていると、例えば目的地までの経路を計算する時に「下から来て左折するルート」を導出できなかったりするかもしれません。

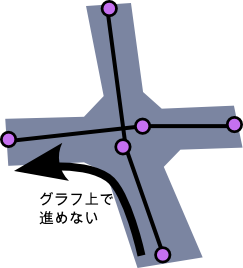
というわけで、もし 2m 以内に点が複数ある場合はそこは交差点とみなして 1 頂点にまとめることにします。 まとめる処理は後でやるとして、ひとまず全ての頂点について「2m 以内に他の頂点があるかどうか」を計算したいですよね！

さてそこで問題です。

Problem (Div1 250)

time limit: 2s

Little Petya は誕生日に平面上の点の集合をプレゼントされました。
Petya は、すべての点について「2m 以内に他の点があるかどうか」を調べるゲームをしていましたが、途中で気持ちよくなって寝てしまいました。
点の座標が与えられるので、あなたが Petya の代わりに最初から調べてください。

Input

vector<pair<double, double>> points

1≦points.size()≦100,000
-10,000≦points[i].first (x座標)≦10,000
-10,000≦points[i].second (y座標)≦10,000
単位は m
任意の半径 5m の円に含まれるの点の個数 ≦ 10

Output

vector<bool> result
result[i] ... points[i] の周囲 2m 以内に他の点(points[j], i≠j)があるかどうか
result.size() should be equals to points.size()

Coding phase start

3...

2...

1...

おわり

回答例

では実際に採用した方法を紹介します。（いろんな方法があると思うので一例です） 空間データ構造としては kd tree, BSP, BVH みたいなのとかいろいろあると思いますが、シンプルで書きやすそうな 2D bucket を使いました。

// データ構造
const double grid_size = 5; // 2m * 2 以上
map<pair<int, int>, vector<pair<double, double> > > data;

空間を正方形のセルに分割したと思って、点は「その点を含むセル」が持つリストに登録します。 具体的にはセルの左下の整数点 pair をキーとして map に点リストを格納します。(右上が X+, Y+ とします)

// grid_size==5 で
// (2.5, 0.0), (5.1, 101.5), (4.0, 4.0) を登録したところ
data = {
 (0, 0) -> [ (2.5, 0.0), (4.0, 4.0) ],
 (1, 20) -> [ (5.1, 101.5) ],
}

クエリは、点の座標から(セルの幅/2, セルの幅/2)を引いた地点のセルと、その右、上、右上の計4セルに含まれる全ての点に対して距離チェックをします。円がセルからはみ出るかもしれないので周辺のセルも見るというわけです。

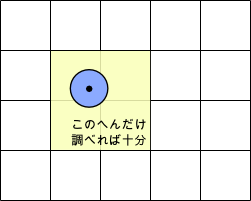
はみ出る対策は、面倒なら無条件に点の座標のセルの周囲 8 個を見るとかでもいいと思います。

セルの 1 辺の長さが 4m 以上であれば、点から 2m 以内の領域は必ずこの4セルに含まれるので、それらをチェックすれば十分です。 また、点の密度に上限があるので、リストに点がたくさん入ってて結局全探索に近くなるといったこともありません。

// クエリ
bool query(double x, double y) {
 const double within = 2.0;
 pair<int, int> base_key(floor(x/grid_size - 0.5), floor(y/grid_size - 0.5));
 int dx[] = {0, 1, 0, 1};
 int dy[] = {0, 0, 1, 1};
 int count = 0;
 for(int i=0;i<4;i++) {
  pair<int, int> key(base_key.first+dx[i], base_key.second+dy[i]);
  if(!data.count(key)) continue;
  for(size_t j=0;j<data[key].size();j++) {
   double lx = x - data[key][j].first;
   double ly = y - data[key][j].second;
   if(lx*lx+ly*ly <= within * within) count++;
  }
 }
 return count > 1; // 自分の点はカウントしない
}

計算量は、点の数を N, 1セルに入るデータ数の平均を M とすると map を引くところが O(log(N/M)), リストを全部見るところが O(M) なのでクエリ全体は O(Mlog(N/M)), 点の密度の上限があるので M を小さな定数とすると O(logN), 実際は定数項が大事とはいえ、まぁいい感じだと思います。

// データ構造の構築
void build(const vector<pair<double, double> >& points) {
 data.clear();
 for(size_t i=0;i<points.size();i++) {
  pair<int, int> key(floor(points[i].first/grid_size), floor(points[i].second/grid_size));
  data[key].push_back(points[i]);
 }
}

// 本体
void solve() {
 build(points);
 for(size_t i=0;i<points.size();i++) {
  result[i] = query(points[i].first, points[i].second);
 }
}

実際のマップデータの処理は python でやっています。さきほどの山手線を含むグラフの場合、総当りで O(N^2) だと終わらなかったのが 2D bucket を使うことで 2.8 秒で終わるようになりました。

2D bucket は他にもこんな所で使っています。大活躍です。

• (マップデータ生成時) ガードレールの生成 アルゴリズム: 道路グラフの辺それぞれについて辺を太くしたような長方形を作って、それらの union の輪郭をポリゴン化するとガードレールの出来上がりです。union を計算するために Clipper を使っています。

• (マップデータ生成時) ジャンプ台を大きな道路のガードレール沿いに設置する処理 アルゴリズム: 細い道のも含むすべてのガードレール沿いに 20m 間隔で候補点を生成して、その後大きな道路上を 50m 間隔で見ていって 20m 以内に候補点があればそこにジャンプ台を設置します。

• (マップデータ生成時) 繁華街のビルの角に看板を設置する処理。看板がよく見えるように道に一番近いビルの角に取り付けます。

アルゴリズム: すべての道上に 10m 間隔で点を設置して、あるビルに含まれるすべての頂点に対して5m以内の点を探す→一番道上の点に近いビルの角に看板を設置します。

• (アプリ実行時) AI車の前方に車がいるかどうか判定する処理 アルゴリズム: AI車は基本的に道路グラフ上をランダムウォークしますが、自車の前方 2m, 4m, 6m, 15m の地点から半径 3m 以内に車がいる場合はブレーキを踏みます。車の位置を適宜更新しつつ、2D bucket のクエリで判定します。

• (アプリ実行時) プレイヤーとの距離が 30m〜100m の歩道上に客を配置して待機させる処理 アルゴリズム: 歩道沿いの候補点をたくさん生成しておいて、プレイヤー近くの候補点を探して客を配置します。プレイヤーに近すぎるといきなり現れたように見えるので 30m 以上遠くの候補点だけ選びます。

• (アプリ実行時) プレイヤーとの距離が 100m〜200m の道路上に AI 車を配置する処理 マップ全体を数千台の車が走っているとすると物理シミュレーションが終わらないので、プレイヤーから 200m くらいの範囲内で車を最大 75 台走らせるようにしています。遠くなった車は GC で回収され、何事もなかったかのようにプレイヤーの近くに配置されます。 アルゴリズム: 道路沿いの候補点をたくさん生成しておいて、プレイヤーからの距離が 100m〜200m の候補点を探して車を配置します。これも近すぎるといきなり現れたように見えるので 100m 以上遠くの点だけを選びます。

• (アプリ実行時) プレイヤーに最も近い場所（駅, 信号機, 店とか）の名前を表示する処理

2D bucket のいいところは、単純でスケールアウトしやすい所だと思います。局所的で場所ごとに独立なデータ構造になってるので、将来もっと広いエリアをサポートする時にマップデータを分割したら 2D bucket のデータ構造もそのまま分割できますし、プレイヤーの移動に合わせてサーバから新たなタイルデータをダウンロードするとか、そもそもマップデータの生成を並列実行するとかも自然にできそうです。

Problem (Div2 475)

time limit: 20s

Fox Ciel は森で見つけた無向グラフをたどるゲームを始めるところです。
Ciel は行き止まりが嫌いなので、行き止まりにくると泣いてしまいます。
Ciel を泣かせないように、与えられたグラフから最低限の頂点と辺を取り除いて、行き止まりを含まないグラフを作ってください。

|V|≦80,000
|E|≦120,000
行き止まりの数≦1000

# alive[v] な頂点だけからなるグラフは行き止まりを含まない
alive ← [True for i in range(len(g))]

# alive なサブグラフ上で次数 1 の頂点がないように alive[i] を False にしていく
changed ← True
while changed:
 changed ← False
 for v in すべての頂点番号:
  while alive[v] かつ v から出る辺のうち、向こう側が live な頂点の個数が 1 なら:
   alive[v] ← False
   changed ← True
   v ← その向こう側の頂点

# alive[v] の頂点だけからなるグラフを構築
old_new_map ← [-1 for i in range(頂点数)]
new_v ← []
new_e ← []
for v in すべての頂点:
 if alive[v]:
  old_new_map[new_v.length] = v
  new_v.append(v)
  new_e.append([])
 for v2 in v から出るすべての頂点:
  if old_new_map[v2] != -1:
   ## 新頂点に入れるべきなので辺を追加する。
   new_e[-1].append(old_new_map[v2])